Welcome to The STORM Count! Today we will be taking a relatively beginner-level look at one of the most useful mathematical concepts when it comes to Magic: the Gathering. It’s particularly useful in a deck that aims to play as few turns as possible, like The EPIC Storm. We are talking about combinatorial probabilities.

Basics of Combinatorics and Probability

In order to talk about combinatorial probabilities, we should establish some baseline knowledge. If you already understand binomial combinations and basic probability, feel free to skip to the next section!

A binomial combination is a formula that takes two inputs. You enter the number of total objects you have to pick from (n) as well as how many objects you are picking (r). The output of the function is the total number of different ways there are to pick r objects from a list of n objects. For example, “3 choose 2” has n = 3 and r = 2, and the output is the number 3, because there are three different groups of two that you can make from three objects. If your objects are A, B, and C, then the combinations are AB, AC, and BC. Binomial combinations do not care about the order of the objects, so CB would not be considered a new combination in this example. This makes sense for our use because the Magic zone we care about, the hand, is an unordered zone. We consider a hand of Thoughtseize, Brainstorm, Dark Ritual to be the same as the hand Dark Ritual, Brainstorm, Thoughtseize. Here is the notation for combinations:

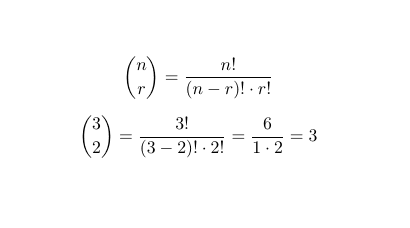
For elementary probabilities, it is important to establish one important assumption: every separate outcome is equally likely. That is, we assume that our deck is perfectly randomly shuffled between each trial. While the quality of shuffles will vary in a real-life scenario, as long as the method of shuffling is not introducing any bias into the ordering of the deck, then this assumption is close enough to true that our numbers will be reliable. Under this assumption, we can calculate the probability of any event by taking the number of outcomes we care about and dividing it by the total number of outcomes. For example, let’s say our opponent just cast Gamble. After they search for a card, they have six cards in their hand. To calculate the probability that they discard the exact card they searched for, we start with the number of outcomes we care about: one, that the card they discarded is the exact card they searched for. Then, we put that in a fraction over the total number of outcomes: six, since they have six cards in their hand. This is what gives us the probability of 1/6, or about 16.7 percent.

Combinatorial Probabilities

We can combine these two concepts. Combinations can be used to determine how many of a particular outcome exists in order to calculate the probability of that outcome.

For example, let’s look at the probability of drawing exactly one Brainstorm in our opening seven-card hand. For the numerator of our probability fraction, we take the number of ways to draw one out of four Brainstorms and multiply that by the number of ways to get six non-Brainstorm cards. Then we divide that by the total number of possible seven-card hands. The calculation looks like this:

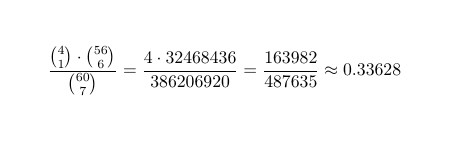
This means you have approximately a 33.6 percent chance of having exactly one Brainstorm in your opening hand.

Let’s try a more complicated example. What is the probability that you will draw exactly one Infernal Tutor, exactly one Lion’s Eye Diamond, and five other cards in your opening hand? Here’s the calculation:

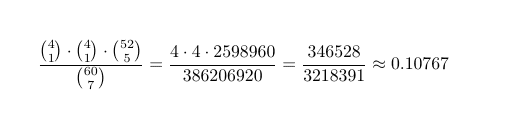
There are lots of ways to use these concepts to generate useful information. This is the concept we used to calculate the probability that your opponent has a Force of Will and a blue card.

Thank you for joining me for this edition of The STORM Count! Hopefully you gained some insight into how we use combinations to determine probabilities of particular opening hands. If you have any questions or ideas for more math you’d like to see discussed, feel free to send me a message on Facebook, email, or Twitter. Until next time, may your Storm counts always be lethal!